Solving Dependent Equations with Graphs and Topological Sorting using math.js

Introduction

In this post, we will explore how to use graphs and topological sorting to solve a set of dependent equations. We will use the math.js library to demonstrate the approach.

Understanding Dependency

A dependency is a relationship between two or more things that requires one or more of them to fulfill its needs.

In the context of equations, a dependency is a relationship between two or more equations that requires one or more of them to be solved before the others can be solved.

For example, consider the following set of equations:

const equations = ["x = 2 * y", "y = 5"];

The first equation depends on the second equation because it requires the value of y to be solved before it can be solved. In other words, the first equation is dependent on the second equation.

Representing Equations with Graphs

A graph is a data structure that consists of a finite set of vertices (nodes), together with a set of edges (links) that connect pairs of vertices. A graph can be either directed or undirected, meaning that the direction of the edges is either taken into account or not.

In the context of dependent equations, a graph can be used to represent the relationships between the equations. We will use a directed graph to represent the dependencies between the equations. Each equation will be represented by a vertex in the graph. An edge will be used to represent a dependency between two equations.

For example, consider the following set of equations:

const equations = [
  { variable: "x", equation: "2*y" },
  { variable: "y", equation: "5" },
  { variable: "s", equation: "y/3" },
  { variable: "z", equation: "s+2y"
]

The following graph can be used to represent the relationships between the equations:

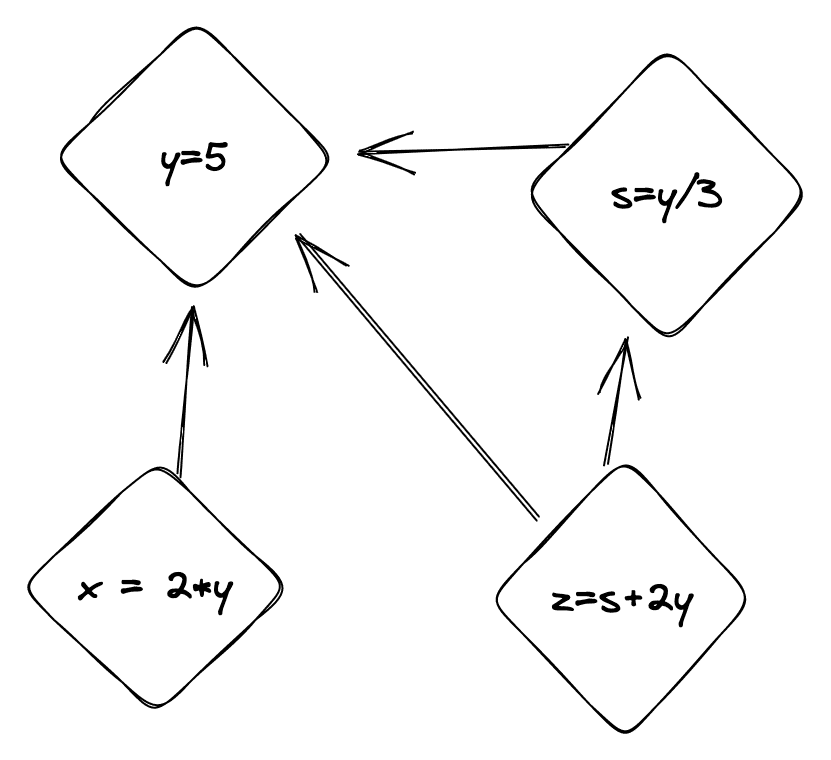
Topological Sorting

Topological sorting is a linear ordering of vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering.

Topological sorting is a way to order the vertices in a graph such that for every edge uv, u comes before v in the ordering. Or in simpler terms, topoligal order makes sure that all the dependencies of a vertex are solved before the vertex itself.

*If you want to learn more about topological sorting, check out this post on GeeksforGeeks.

For example, consider the previous graph. A topological ordering of the graph might look like this:

const topologicalOrdering = ["y", "x", "s", "z"];

Real-world Example

Now that we have a basic understanding of graphs and topological sorting, let’s see how we can use them to solve a set of dependent equations.

First we will need to define the structure of the graph. We will use the following types to represent vertices and edges in the graph:

type Vertex = {
  variable: string;
  equation: string;
};

type Edge = {
  from: Vertex;
  to: Vertex;
};

type Graph = {
  vertices: Vertex[];
  edges: Edge[];
};

The Vertex type represents a node in the graph (equation). The Edge type represents a dependency between two equations. The Graph type represents the graph itself, which consists of a set of vertices and a set of edges. In our case, the graph represents a set of dependent equations.

Next, we will need to define a function to create a graph from a set of equations.

type Equation = {
  variable: string;
  equation: string;
}

function createGraph(equations: Equation[]): Graph {
  const vertices = equations.map(item => ({
    token: item.token,
    equation: item.equation,
  }))

  const edges = equations
    .map(item => {
       // parse the equation to get the dependencies
      const dependencies = parseEquation(item.equation)

      return dependencies.map(dependency => ({
        from: dependency,
        to: item.token,
      }))
    })
    .flat()

  return {vertices, edges}
}

function parseEquation(equation: string) {
  let symbols: string[] = []
  let functions: string[] = []

  math.parse(equation).traverse(node => {
      if (node.isSymbolNode) {
        symbols.push(node.name)
      } else if (node.isFunctionNode) {
        functions.push(node.name)
      }
  })

  return = difference(symbols, functions)
}

function difference(a: string[], b: string[]) {
  return a.filter(x => !b.includes(x))
}

Ok, so it looks like a lot of code, so here are the important parts:

1. We are defining a function called createGraph that takes a set of equations and returns a graph. All it does is create a vertex for each equation and create an edge for each dependency between the equations.
2. The parseEquation function is used to parse the equation and get the dependencies using the math.js library.
3. In order to only get the variables from the equation, we are using the difference function to remove the function calls from the list of symbols.

Now that we have a function to create a graph from a set of equations, we can use topological sorting to order the equations in the graph.

function topologicalSort(graph: Graph): Vertex[] {
  const vertices = graph.vertices.map((vertex) => vertex.token);
  const sorted: string[] = [];
  const visited: Record<string, boolean> = {};

  function visit(vertex: string) {
    if (visited[vertex]) {
      return;
    }

    visited[vertex] = true;

    const edges = graph.edges.filter((edge) => edge.from === vertex);

    for (const edge of edges) {
      visit(edge.to);
    }

    sorted.push(vertex);
  }

  for (const vertex of vertices) {
    visit(vertex);
  }

  return sorted;
}

The topologicalSort function takes a graph and returns a topological ordering of the equations in the graph. It uses a depth-first search to traverse the graph and visit each vertex. For each vertex, it marks the vertex as visited and visits all the vertices that are dependent on the current vertex. This process continues until all the vertices have been visited.

Now that we have a function to create a graph and a function to order the equations in the graph, we can use these functions to solve the equations.

function solveEquations(equations: Equation[]): Record<string, number> {
  const graph = createGraph(equations);
  const sorted = topologicalSort(graph);

  const results: Record<string, number> = {};

  for (const vertex of sorted) {
    const equation = graph.vertices.find(
      (item) => item.token === vertex
    ).equation;
    results[vertex] = math.evaluate(equation, values);
  }

  return results;
}

The solveEquations function takes a set of equations and returns the values of the variables. It uses the createGraph function to create a graph from the equations and the topologicalSort function to order the equations in the graph. Then it uses the math.js library to evaluate the equations and return the values of the variables. After each equation is evaluated, the values of the variables are stored in the results object. This fact, combined with the fact that the equations are ordered, means that the values of the variables are available when evaluating the equations.